Eksperimen Potong Kertas Proposisi Euklides I.47

Ini adalah percobaan sederhana –atau boleh disebut juga kegiatan iseng– yang saya lakukan untuk menunjukkan pembuktian proposisi nomor 47 pada Buku I Elemen Euklides.

[**Tulisan lebih lanjut tentang proposisi I.47 dan Euklides dapat anda baca pada entri-entri berikut ini: "Proposisi Euclid I.47: Segitiga Freemasonry"; "Bapak Geometri Euklides(Euclid) yang Misterius & Euclid's Element"; "Pembuktian Matematika dan Q.E.D. (Quod Erat Demonstrandum)"**]

(1) Langkah awal, saya menyiapkan gambar proposisi tersebut.

**Bila anda juga tertarik melakukan percobaan ini, anda bisa memakai gambar di atas, atau googling gambar proposisi Euklides I.47 yang lainnya.**

Proposisi Euklides I.47

(2) Kemudian saya mencetak beberapa copy gambar tersebut satu halaman penuh A4.

Langkah kedua

(3) Saya warnai segitiga ABD sebanyak dua lembar copy dengan pensil warna. Sebenarnya tentu saja saya bisa mewarnai secara digital sebelum saya mencetak gambar, namun saya memilih menggunakan cara ini semata karena melihat pensil warna saya tak terpakai.

Langkah ketiga

(4) Setelahnya saya memotong segitiga ABD yang telah diwarnai.

Langkah keempat

(5) Lalu saya memutar 180^o salah satu segitiga ABD, dan menggabungkan kedua segitiga ABD.

Langkah kelima

(6) Pada gabungan kedua segitiga ABD, saya memotong bagian segitiga atas seperti yang ditunjukkan pada gambar di bawah ini.

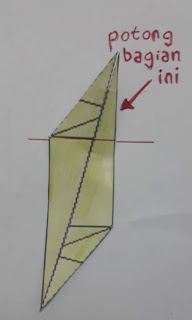Langkah keenam

(7) Saya memindahkan potongan pada langkah (6) ke bawah, sehingga gabungan segitiga ABD membentuk persegi panjang.

Langkah ketujuh

(8) Selanjutnya saya menaruh persegi panjang pada langkah (7) ke atas segiempat BL. Segiempat BL akan tertutup secara penuh, membuktikan pernyataan “Luas segiempat BL sama dengan dua kali luas segitiga ABD.”

Langkah kedelapan

(9) Anda bisa melakukan langkah potong-potong kertas serupa untuk membuktikan pernyataan lain, misalnya pernyataan: luas persegi GB sama dengan luar segiempat BL, luas segiempat CL sama dengan luas persegi HACK, dan sebagainya.

COCOKLOGI !!!!!